DNN with backpropagation in C++, part 8
Implementing convolution layer in C++
Definitions
Continuos convolution of two functions f and g is defined as:
\[(f * g)(t) = \int_{-\infty}^{\infty} f(\mathcal{\tau})g(t-\mathcal{\tau}) \partial \mathcal{\tau}\]Discrete convolution is defined by the sum:
\[(f * g)(i) = \sum_{m=-\infty}^{\infty} f(m) g(i-m)\]The kernel in convoution formula above is flipped. The reason for this is to maintain commutative property:
\[f * g = g * f\]Commutativity of convolution is not required in deep learning frameworks, and it’s common to use simpler cross-corellation instead of convolution:
\[y(i) = \sum_{m=0}^{M-1} f(m) g(m)\]For 2-D case:
\[f(i, j) = \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f(m, n) g(m, n)\]Example of discrete 2D convolution of 5x5 input (light blue) with 3x3 kernel (dark blue), producing 3x3 output (green)
Kernel:
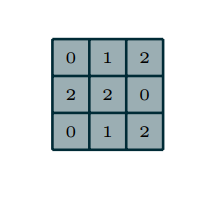
Convolution:
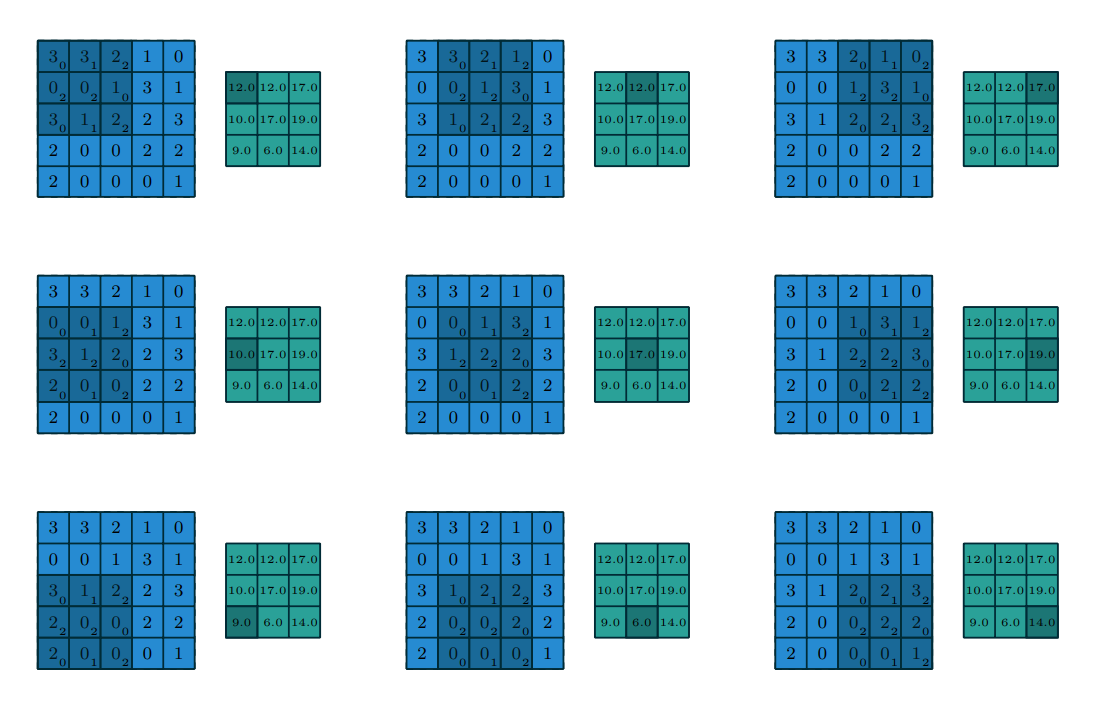
Convolution illustration is from “A guide to convolution arithmetic for deep learning”, by Vincent Dumoulin, Francesco Visin
Forward path for convolution layer
Convolution layer output \(\hat Y\) is:
\[\hat Y = W * X\]W is convolution kernel of size K:
\[W^\intercal = \left( \begin{array}{ccc} w_{0} & w_{1} & \ldots & w_{K-1} \\ \end{array} \right)\]X is input vector of size N:
\[X^\intercal = \left( \begin{array}{ccc} x_{0} & x_{1} & \ldots & x_{N-1} \\ \end{array} \right)\]Convolution as a matrix multiplication
1D convolution operator can be represented as a matrix multiplication of Toeplitz matrix representation of weights \(T_{w}\), and input X:
\[\hat Y = T_{w} X = \left( \begin{array}{ccc} w_{0} & w_{1} & w_{k-1} & 0 & \ldots & 0 \\ 0 & w_{0} & w_{1} & w_{k-1} & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots & 0 \\ 0 & \ldots & w_{0} & w_{1} & \ldots & w_{k-1} \\ \end{array} \right) \left( \begin{array}{ccc} x_{0} \\ x_{1} \\ \ldots \\ x_{n-1} \\ \end{array} \right)\]Convolution can also be represented as matrix multiplication of Toeplitz matrix of input X and weights W
\[\hat Y = T_{x} W = \left( \begin{array}{ccc} x_{0} & x_{1} & \ldots & x_{k-1} \\ x_{1} & x_{2} & \ldots & x_{k} \\ \vdots & \vdots & \ldots & \ldots \\ x_{n-k} & x_{n-k+1} & \ldots & x_{n-1} \\ \end{array} \right) \left( \begin{array}{ccc} w_{0} \\ w_{1} \\ \ldots \\ w_{k-1} \\ \end{array} \right)\]Error backpropagation
We’d like to minimize the error difference between out network output and expected output,
by adjusting convolution layer weights by error E gradient \(\frac {\partial E(\hat Y)} {\partial W}\)
Using chain rule:
\[\frac {\partial E } {\partial W} = \frac {\partial E} {\partial \hat Y} \frac {\partial \hat Y} {\partial W}\]Using multiplication \(T_{x} W\) for convolution, we can see that partial derivative of convolution \(\frac {\partial \hat Y} {\partial W}\) is matrix \(T_{x}\):
\[\frac {\partial \hat Y} {\partial W} = \frac {\partial (W * X)} {\partial W} = \frac {\partial (T_{x} W)} {\partial W} = T_{x}\]Error derivative \(\frac {\partial E} {\partial \hat Y}\) is a Jacobian:
\[\frac {\partial E} {\partial \hat Y} = \left( \begin{array}{ccc} \partial \hat y_{0} & \partial \hat y_{1} & \ldots & \partial \hat y_{n-1} \\ \end{array} \right)\]Kernel weight gradient \(\frac {\partial E} {\partial W}\) becomes convolution of gradient \(\frac {\partial E} {\partial \hat Y}\) and input \(X\) :
\[\frac {\partial E} {\partial W} = \frac {\partial E} {\partial \hat Y} T_{x} = \left( \begin{array}{ccc} \partial \hat y_{0} & \partial \hat y_{1} & \ldots & \partial \hat y_{n-1} \\ \end{array} \right) \left( \begin{array}{ccc} x_{0} & x_{1} & \ldots & x_{k-1} \\ x_{1} & x_{2} & \ldots & x_{k} \\ \vdots & \vdots & \ldots & \ldots \\ x_{n-k} & x_{n-k+1} & \ldots & x_{n-1} \\ \end{array} \right) = \frac {\partial E} {\partial \hat Y} * X\]We also need to find output gradient update \(\frac {\partial E (\hat Y) } {\partial X}\) used in backpropagation for the previous layer
\[\frac {\partial E (\hat Y) } {\partial X} = \frac {\partial E} {\partial \hat Y} \frac {\partial \hat Y} {\partial X}\]Replacing convolution with multilication by Toeptlitz for kernel weights:
\[\frac {\partial \hat Y} {\partial X} = \frac {\partial (T_{w} X)} {\partial X} = T_{w}\] \[\frac {\partial E (\hat Y) } {\partial X} = J T_{w}^\intercal = \left( \begin{array}{ccc} \partial \hat y_{0} & \partial \hat y_{1} & \ldots & \partial \hat y_{n} \\ \end{array} \right) \left( \begin{array}{ccc} w_{0} & w_{1} & w_{k-1} & 0 & \ldots & 0 \\ 0 & w_{0} & w_{1} & w_{k-1} & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots & 0 \\ 0 & \ldots & w_{0} & w_{1} & \ldots & w_{k-1} \\ \end{array} \right)\]Output gradient \(\frac {\partial E (\hat Y) } {\partial X}\) is convolution of error gradient J and flipped kernel weighs:
\[\frac {\partial E (\hat Y) } {\partial X} = J * FLIP(W)\]Bias
Bias B is added to convolution output:
\[Y = W*X+b\]Using chain rule to find bias gradient:
\[\frac {\partial E} {\partial b} = \frac {\partial E} {\partial \hat Y} \frac {\partial \hat Y} {\partial b}\]Derivative \(\partial b\) is:
\[\frac {\partial \hat Y} {\partial b} = \frac {\partial (T_{W} X + b)} {\partial b} = \left( \begin{array}{ccc} 1 \\ 1 \\ \ldots \\ 1 \end{array} \right)\]Bias gradient \(\partial b\) is a sum of error gradients:
\[\partial b = \left( \begin{array}{ccc} \partial \hat y_{0} & \partial \hat y_{1} & \ldots & \partial \hat y_{n-1} \\ \end{array} \right) \left( \begin{array}{ccc} 1 \\ 1 \\ \ldots \\ 1 \end{array} \right) = \sum_{i} \partial \hat y_{i}\]Backpropagation for 2D convolution layer
Backpropagation for 2D convolution layer is similar to the 1D case, except doubly block Toeplitz matrices are used for input and kernel representation.
Multiple input and output channels
In case of multiple input channels , convolution channel output is a sum of convolutions for each input channel.
Illustration of multiple channel convolution from “A guide to convolution arithmetic for deep learning”, by Vincent Dumoulin, Francesco Visin. :
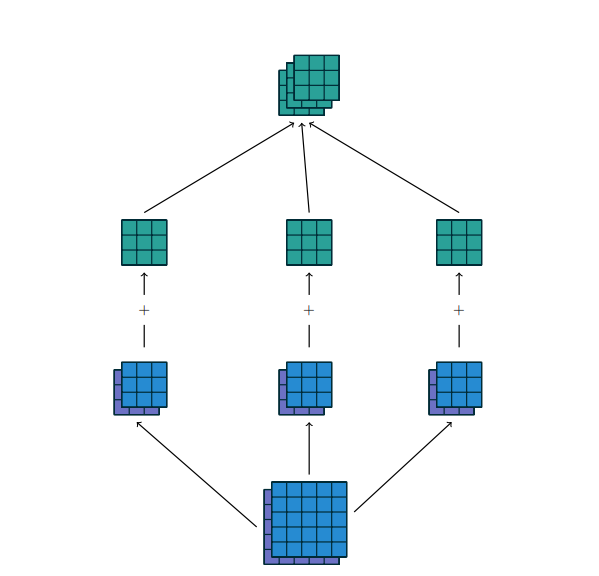
From basic differentiation rules, derivative of a sum of functions is the sum of their derivatives. Output gradient and convoluton kernel weight update will be sums of corresponding dervatives over output channels.
Now let’s implement single convolution layer DNN
Python implementation will be used for validating C++ convolution code in the following section
import tensorflow as tf
from tensorflow.keras.layers import Dense, Softmax
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras import backend as K
import numpy as np
np.set_printoptions(formatter={'float': '{: 0.3f}'.format}, edgeitems=10, linewidth=180)
# DNN parameters used in this example
# 5x5 input plane
input_height = 5
input_width = 5
# 1 channel input
channels_in = 2
# 2 chnnel output
channels_out = 1
# 3x3 kernel size
kernel_size = 3
# stride of 1
stride = 1
# conv layer weights initializer is:
# [1, 2, ..., kernel_size * kernel_size * channels_in * channels_out]
kernel_weights_num = kernel_size * kernel_size * channels_in * channels_out
conv_weights = np.reshape(np.linspace(start=1,
stop=kernel_weights_num,
num=kernel_weights_num),
(channels_out, channels_in, kernel_size, kernel_size))
# conv layer bias initializer is array [channels_out, channels_out-1, ..., 1]
conv_bias = np.linspace(start=channels_out, stop=1, num=channels_out)
# Conv layer weights are in Height, Width, Input channels, Output channels (HWIO) format
conv_weights = np.transpose(conv_weights, [2, 3, 1, 0])
# generate input data
input_shape = (1, input_height, input_width, channels_in)
input_size = input_height * input_width * channels_in
x = np.reshape(np.linspace(start = input_size , stop = 1, num = input_size),
(1, channels_in, input_height, input_width))
# input data is in Batch, Height, Width, Channels (BHWC) format
x = np.transpose(x, [0, 2, 3, 1])
# Create sequential model with 1 conv layer
# Conv layer has bias, no activation stride of 1, 3x3 kernel, zero input padding
# for output to have same dimension as input
model = tf.keras.Sequential()
model.add(tf.keras.layers.Conv2D(filters=channels_out,
kernel_size=kernel_size,
strides=stride,
activation=None,
use_bias=True,
data_format="channels_last",
padding="same",
weights=[conv_weights, conv_bias]))
# Builds the model based on input shapes received
model.build(input_shape=input_shape)
# Use MSE for loss function
loss_fn = tf.keras.losses.MeanSquaredError()
# print input data in BCHW format
print(f"input x:\n{np.squeeze(np.transpose(x, [0, 3, 1, 2]))}")
# Print Conv kernel in OIHW format
print(f"conv kernel weights:\n "\
f"{np.transpose(model.trainable_variables[0].numpy(), [3, 2, 0, 1])}")
# print Conv bias
print(f"conv kernel bias: {model.trainable_variables[1].numpy()}")
# Create expected output
y_true = np.ones(shape=(1, input_height, input_width, channels_out))
# SGD update rule for parameter w with gradient g when momentum is 0:
# w = w - learning_rate * g
# For simplicity make learning_rate=1.0
optimizer = tf.keras.optimizers.SGD(learning_rate=1.0, momentum=0.0)
# Get model output y for input x, compute loss, and record gradients
with tf.GradientTape(persistent=True) as tape:
xt = tf.convert_to_tensor(x)
tape.watch(xt)
y = model(xt)
loss = loss_fn(y_true, y)
# dloss_dy is error gradient w.r.t. DNN output y
dloss_dy = tape.gradient(loss, y)
# dloss_dx is error gradient w.r.t DNN input x
dloss_dx = tape.gradient(loss, xt)
# Update DNN weights with gradients
grad = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grad, model.trainable_variables))
# print model output in BCHW format
print(f"output y:\n{np.squeeze(np.transpose(y, [0, 3, 1, 2]))}")
# print loss
print("loss: {}".format(loss))
# print dloss_dy: error gradient w.r.t. DNN output y, in BCHW format
print("dloss_dy:\n{}".format(np.squeeze((np.transpose(dloss_dy, [0, 3, 1, 2])))))
# print dloss_dx: error gradient w.r.t DNN input x, , in BCHW format
print("dloss_dx:\n{}".format(np.squeeze(np.transpose(dloss_dx, [0, 3, 1, 2]))))
# print updated conv layer kernel and bias weights
print(f"updated conv kernel:\n "\
f"{np.transpose(model.trainable_variables[0].numpy(), [3, 2, 0, 1])}")
print(f"updated conv bias: {model.trainable_variables[1].numpy()}")Output after running Python code:
$ python3 conv8.py
input x:
[[[ 50.000 49.000 48.000 47.000 46.000]
[ 45.000 44.000 43.000 42.000 41.000]
[ 40.000 39.000 38.000 37.000 36.000]
[ 35.000 34.000 33.000 32.000 31.000]
[ 30.000 29.000 28.000 27.000 26.000]]
[[ 25.000 24.000 23.000 22.000 21.000]
[ 20.000 19.000 18.000 17.000 16.000]
[ 15.000 14.000 13.000 12.000 11.000]
[ 10.000 9.000 8.000 7.000 6.000]
[ 5.000 4.000 3.000 2.000 1.000]]]
conv kernel weights:
[[[[ 1.000 2.000 3.000]
[ 4.000 5.000 6.000]
[ 7.000 8.000 9.000]]
[[ 10.000 11.000 12.000]
[ 13.000 14.000 15.000]
[ 16.000 17.000 18.000]]]]
conv kernel bias: [ 1.000]
output y:
[[ 2693.000 3761.000 3629.000 3497.000 2165.000]
[ 3043.000 4183.000 4012.000 3841.000 2335.000]
[ 2443.000 3328.000 3157.000 2986.000 1795.000]
[ 1843.000 2473.000 2302.000 2131.000 1255.000]
[ 845.000 1097.000 1001.000 905.000 509.000]]
loss: 7139752.5
dloss_dy:
[[ 215.360 300.800 290.240 279.680 173.120]
[ 243.360 334.560 320.880 307.200 186.720]
[ 195.360 266.160 252.480 238.800 143.520]
[ 147.360 197.760 184.080 170.400 100.320]
[ 67.520 87.680 80.000 72.320 40.640]]
dloss_dx:
[[[ 3101.280 5677.200 6327.360 5596.080 3838.720]
[ 7040.401 12163.680 13369.680 11648.159 7682.320]
[ 6822.720 11647.439 12674.881 10928.880 7120.800]
[ 5176.560 8722.080 9370.800 7970.400 5119.600]
[ 3251.520 5360.400 5660.640 4726.320 2973.280]]
[[ 12948.000 21024.000 22827.600 19616.639 12359.199]
[ 21040.799 33936.480 36686.879 31381.918 19643.680]
[ 19283.760 30925.441 33125.762 28068.479 17443.439]
[ 13833.120 22027.682 23317.918 19513.439 12013.601]
[ 7754.400 12240.000 12790.800 10556.160 6426.399]]]
updated conv kernel:
[[[[-130106.523 -156338.812 -133827.078]
[-166008.953 -198697.391 -169492.078]
[-139199.719 -166136.000 -141313.250]]
[[-55509.520 -65401.797 -54670.078]
[-65315.961 -76280.398 -63183.082]
[-45522.719 -52423.000 -42692.238]]]]
updated conv bias: [-4895.320]C++ implementation
Include headers
#include <cstdio>
#include <vector>
#include <array>
#include <algorithm>
#include <array>
#include <iterator>
#include <variant>
#include <random>
using namespace std;N-dimentional array recursive template, which will be used in convolution and flatten DNN layers.
/*
* N-dimentional array definition
*/
template <typename T, std::size_t N, std::size_t... Dims>
struct ndarray
{
/*
* Array type and size
*/
using type = std::array<typename ndarray<T, Dims...>::type, N>;
static constexpr std::size_t size = {(Dims * ... * N)};
/*
* Get array value at index
*/
static const T& ndarray_at(const typename ndarray<T, N, Dims...>::type & x, size_t index)
{
auto size = ndarray<T, Dims...>::size;
size_t outer_index = index / size;
size_t inner_index = index % size;
return ndarray<T, Dims...>::ndarray_at(x[outer_index], inner_index);
}
/*
* Reference to array value at index
*/
static T& ndarray_at(typename ndarray<T, N, Dims...>::type & x, size_t index)
{
/*
* For explanation, see "Avoid Duplication in const and Non-const Member Function"
* Effective C++ by Scott Meyers
*/
return const_cast<T&>(ndarray_at(static_cast<const ndarray<T, N, Dims...>::type& >(x), index));
}
};
/*
* 1 dimentional array definition
* terminating N-dimentional array recursive ndarray<>
*/
template <typename T, size_t N>
struct ndarray<T, N> {
using type = std::array<T, N>;
static constexpr std::size_t size = {N};
static const T& ndarray_at(const std::array<T, N>& x, size_t index)
{
return x[index];
}
static T& ndarray_at(std::array<T, N>& x, size_t index)
{
return const_cast<T&>(ndarray_at(x, index));
}
};Helper functions for N dimentional arrays:
Convolution of N dimentional arrays.
/*
* Compute convolution of N dimentional inputs x and w
*/
/*
* Inner product of 1 dimentional arrays X and W, terminating
* recursive N dimentional inner_product_nd() definition.
*/
template<typename T, std::size_t size_x, std::size_t size_w>
static T inner_product_nd(const std::array<float, size_x>& x,
const std::array<float, size_w>& w,
const int idx)
{
const int i = idx;
const int pad_left = (i < 0) ? (- i) : 0;
const int pad_right =
(i > static_cast<int>(size_x) - static_cast<int>(size_w)) ?
(i - static_cast<int>(size_x) + static_cast<int>(size_w)) : 0;
return std::inner_product(w.begin() + pad_left,
w.end() - pad_right,
x.begin() + pad_left + i,
static_cast<T>(0));
}
/*
* Definiton of inner product between N dimentional
* input X and N-dimentional input W
* Recursively unwind X and W untile we get to 1 dimentinal array.
* Then compute 1 dimentional inner product.
*/
template<typename T,
typename type_x, std::size_t size_x,
typename type_w, std::size_t size_w,
typename... Idx>
static float inner_product_nd(const std::array<type_x, size_x>& x,
const std::array<type_w, size_w>& w,
const int idx_outer,
Idx... idx_inner)
{
const int i = idx_outer;
const int pad_left = (i < 0) ? (- i) : 0;
const int pad_right =
(i > static_cast<int>(size_x) - static_cast<int>(size_w)) ?
(i - static_cast<int>(size_x) + static_cast<int>(size_w)) : 0;
float sum = 0;
for (ssize_t k = pad_left; k < (static_cast<int>(size_w) - pad_right); k ++)
{
sum += inner_product_nd<T>(x[i+k], w[k], idx_inner...);
}
return sum;
};
/*
* Convolution of N -dimentional input X and N-dimentional kernel W
* Output convolution result to Y
* pad_size is padding for input X on both sides in each dimension
*/
/*
* Recursion on output N-D array Y until we get to scalar value
*/
template<typename T, int pad_size,
typename Y,
std::size_t N,
typename X,
typename W,
typename... Idx>
void convolution_nd(std::array<Y, N> & y,
const X & x,
const W & w,
Idx... idx)
{
for (int i = 0; i < static_cast<int>(N); i++)
{
convolution_nd<T, pad_size>(y[i], x, w, idx..., i - pad_size);
}
}
/*
* Terminating recursive convolution_nd(...) definition above.
* Compute inner produt of N-dimentional input X at offsets Idx, and kernel W
*/
template<typename T,
int pad_size,
typename X,
typename W,
typename... Idx>
void convolution_nd(T & y,
const X & x,
const W & w,
Idx... idx)
{
y += inner_product_nd<T>(x, w, idx...);
}Apply generic function to each value in N dimentional array
/*
* Apply function for each item in N-dimentional container
*/
template<typename T, typename F>
auto for_each_nd(T& x, F func)
{
func(x);
}
template<typename T, std::size_t N, typename F>
auto for_each_nd(std::array<T, N>& x, F func)
{
std::for_each(x.begin(), x.end(), [func](auto& x_i)
{
for_each_nd(x_i, func);
});
}Pretty printing of N dimentional array
/*
* N-dimentional array print function
*/
auto print_n(const float& x, const char* fmt)
{
printf(fmt, x);
}
template<typename T>
auto print_n(const T& x, const char* fmt="%7.2f ")
{
std::for_each(x.begin(), x.end(),
[fmt](const auto& xi)
{
print_n(xi, fmt);
});
printf("\n");
}Generators used in weights, biases, and input initialization
/*
* Incremental and decremental generators
*/
template<int initial_value = 0, typename T=float>
auto generate_inc = [](T& x) { static int i = initial_value; x = static_cast<T>(i++);};
template<int initial_value = 0, typename T=float>
auto generate_dec = [](T& x) { static int i = initial_value; x= static_cast<T>(i--);};
/*
* Constant value generator
*/
template <typename T=float>
struct generate_const
{
T value = 0;
generate_const(T init_value=0)
{
value = init_value;
}
void operator()(T& x)
{
x = value;
}
};Mean squared error MSE for loss functions
/*
* Mean Squared Error loss class
* Parameters:
* num_inputs: number of inputs to MSE function.
* T: input type, float by defaut.
*/
template<size_t num_inputs, typename T = float>
struct MSE
{
/*
* Forward pass computes MSE loss for inputs y (label) and yhat (predicted)
*/
static T forward(const array<T, num_inputs>& y, const array<T, num_inputs>& yhat)
{
T loss = transform_reduce(y.begin(), y.end(), yhat.begin(), 0.0, plus<T>(),
[](const T& left, const T& right)
{
return (left - right) * (left - right);
}
);
return loss / static_cast<T>(num_inputs);
}
/*
* Backward pass computes dloss/dy for inputs y (label) and yhat (predicted)
*
* loss = sum((yhat[i] - y[i])^2) / N
* i=0...N-1
* where N is number of inputs
*
* d_loss/dy[i] = 2 * (yhat[i] - y[i]) * (-1) / N
* d_loss/dy[i] = 2 * (y[i] - yhat[i]) / N
*
*/
static array<T, num_inputs> backward(const array<T, num_inputs>& y,
const array<T, num_inputs>& yhat)
{
array<T, num_inputs> de_dy;
transform(y.begin(), y.end(), yhat.begin(), de_dy.begin(),
[](const T& left, const T& right)
{
return 2 * (right - left) / num_inputs;
}
);
return de_dy;
}
};We’ll introduce Flatten layer to reshape 2D output from convolution to one dimension array expected by the error function
Backpropagation for this layer is inverse reshape from 1D to 2D
/*
* Flatten class converts input N-dimentional array to 1 dimentional array
* in the forward() call, and applies inverse 1-D to N-D conversion in the backward() call
*/
template<typename T = float,
std::size_t channels = 1,
std::size_t... Dims>
struct Flatten
{
typedef ndarray<float, channels, Dims...> input_array;
typedef input_array::type input_type;
typedef array<T, input_array::size> output_type;
static constexpr std::size_t size_inner = {(Dims * ...)};
output_type forward(const input_type& x)
{
output_type y;
for (size_t i = 0; i < channels; i++)
{
for (size_t j = 0; j < size_inner; j++)
{
y[i+j*channels] = ndarray<float, Dims...>::ndarray_at(x[i], j);
}
}
return y;
}
input_type backward(const output_type& y)
{
input_type x;
for (size_t i = 0; i < channels; i++)
{
for (size_t j = 0; j < size_inner; j++)
{
ndarray<float, Dims...>::ndarray_at(x[i], j) = y[i+j*channels];
}
}
return x;
}
};2D convolution layer class template
2D convolution layer class template parameters are: input height and width, number of input and output channels, kernel size, stride (currently unused), optional bias,and optional weight initializers.
/*
* 2D convolution class template
*/
template<int channels_out, /* output channels */
int channels_inp, /* input channels */
int input_height, /* input height */
int input_width, /* input width */
int kernel_size = 3, /* kernel size */
int stride = 1, /* stride (currently unused) */
bool use_bias = false, /* bias enable flag */
typename T = float, /* convolution data type */
void (*weights_initializer)(T&) = generate_const<T>(), /* initializer function for weights */
void (*bias_initializer)(T&) = generate_const<T>()> /* initializer function for biases */
struct Conv2D
{
/*
* Conv layer input
*/
typedef ndarray<T, channels_inp, input_height, input_width> input_array;
typedef input_array::type conv_input;
/*
* Conv layer output
* Assume output dimention is the same as input dimention
* This is equivalet to padding="same" in Keras
*/
static const int output_width = input_width;
static const int output_height = input_height;
typedef ndarray<T, channels_out, output_height, output_width> output_array;
typedef output_array::type conv_output;
/*
* Input zero padding required for "same" convolution padding mode.
*/
static const int pad_size = kernel_size / 2;
static constexpr size_t ndims = 2;
using ssize_t = std::make_signed_t<std::size_t>;
/*
* Weights are in Output, Input, Height, Width (OIHW) format
* dw is weights gradient
*/
typedef ndarray<T, channels_out, channels_inp, kernel_size, kernel_size>::type conv_weights;
conv_weights weights;
conv_weights dw;
/*
* Bias is 1D vector
* db is bias gradient
*/
typedef array<T, channels_out> conv_bias;
conv_bias bias;
conv_bias db;
/*
* Default convolution constructor
*/
Conv2D()
{
for_each_nd(weights, *weights_initializer);
for_each_nd(bias, *bias_initializer);
for_each_nd(dw, generate_const<T>());
for_each_nd(db, generate_const<T>());
}
/*
* Forward path computes 2D convolution of input x and kernel weights w
*/
conv_output forward(const conv_input& x)
{
conv_output y;
for (int output_channel = 0; output_channel < channels_out; output_channel++)
{
for_each_nd(y[output_channel], generate_const{use_bias * bias[output_channel]});
}
for (int output_channel = 0; output_channel < channels_out; output_channel++)
{
for (int input_channel = 0; input_channel < channels_inp; input_channel++)
{
convolution_nd<T, pad_size>(y[output_channel], x[input_channel], weights[output_channel][input_channel]);
}
}
return y;
}
/*
* Backward path computes:
* - weight gradient dW
* - bias gradient dB
* - output gradient dX
*/
conv_input backward(const conv_input& x, const conv_output& grad)
{
/*
* Compute weight gradient dw
*/
for (int output_channel = 0; output_channel < channels_out; output_channel++)
{
for (int input_channel = 0; input_channel < channels_inp; input_channel++)
{
convolution_nd<T, pad_size>(dw[output_channel][input_channel], x[input_channel], grad[output_channel]);
}
}
/*
* Compute bias gradient db
*/
for (int output_channel = 0; output_channel < channels_out; output_channel++)
{
db[output_channel] += std::accumulate(grad[output_channel].cbegin(),
grad[output_channel].cend(),
static_cast<T>(0),
[](auto total, const auto& grad_i)
{
return std::accumulate(grad_i.cbegin(),
grad_i.cend(),
total);
});
}
/*
* Compute output gradient dX
*/
conv_input dx = {};
for (int output_channel = 0; output_channel < channels_out; output_channel++)
{
for (int input_channel = 0; input_channel < channels_inp; input_channel++)
{
auto weights_rot180 = weights[output_channel][input_channel];
rotate_180<T, kernel_size>(weights_rot180);
convolution_nd<T, pad_size>(dx[input_channel], grad[output_channel], weights_rot180);
}
}
return dx;
}
/*
* Apply previously computed weight and bias gradients dW, dB, reset gradients to 0
*/
void train(float learning_rate)
{
/*
* compute w = w - learning_rate * dw
*/
for (int input_channel = 0; input_channel < channels_inp; input_channel++)
{
for (int output_channel = 0; output_channel < channels_out; output_channel++)
{
for (size_t i = 0; i < kernel_size; i++)
{
for (size_t j = 0; j < kernel_size; j++)
{
auto weight_update = learning_rate * dw[output_channel][input_channel][i][j];
weights[output_channel][input_channel][i][j] -= weight_update;
}
}
}
}
/*
* compute bias = bias - learning_rate * db
*/
if (use_bias)
{
for (int output_channel = 0; output_channel < channels_out; output_channel++)
{
bias[output_channel] -= learning_rate * db[output_channel];
}
}
/*
* Reset accumulated dw and db
*/
reset_gradients();
}
/*
* Reset accumulated weight and bias gradients
*/
void reset_gradients()
{
for_each_nd(dw, generate_const<T>());
for_each_nd(db, generate_const<T>());
}
/*
* Rotate square 2D array by 180 degrees
*/
template<typename X, std::size_t N>
void rotate_180(typename ndarray<X, N, N>::type& x)
{
for (std::size_t i = 0; i < N / 2; i++)
{
for (std::size_t j = 0; j < N; j++)
{
auto t = x[i][j];
x[i][j] = x[N - i - 1][N - j - 1];
x[N - i - 1][N - j - 1] = t;
}
}
/*
* Odd dimension
*/
if (N & 1)
{
for (std::size_t j = 0; j < N / 2; j++)
{
auto t = x[N / 2][j];
x[N / 2][j] = x[N / 2][N - j - 1];
x[N / 2][N - j - 1] = t;
}
}
}
};Main function
main() creates a neural net consisting of one convolution, one flattent, and mean squared error loss.
After executing forward path, it prints output and loss.
Then it backpropagates the loss and prints updated layer weights and bias values.
One can also verify that printed updated weights and biases match those in the earlier Python implementation.
/*
* DNN train and validation loops are implemented in the main() function.
*/
int main(void)
{
const int input_height = 5;
const int input_width = 5;
const int channels_in = 2;
const int channels_out = 1;
const int kernel_size = 3;
using input_type = ndarray<float, channels_in, input_height, input_width>;
input_type::type x = {};
initialize(x, gen_dec<input_height * input_width * channels_in>);
std::array<float, input_height * input_width * channels_out> y_true;
std::fill(y_true.begin(), y_true.end(), 1.0);
/*
* Create DNN layers and the loss
*/
Conv2D<channels_out, /* number of output channels */
channels_in, /* number of input channels */
input_height, /* input height */
input_width, /* input width */
kernel_size, /* convolution kernel size */
1, /* stride */
true, /* use_bias flag */
float, /* conv data type */
gen_inc<1>, /* initialier for kernel weights */
gen_dec<channels_out> /* initialier for bias weights */
> conv;
Flatten<float, channels_out, input_height, input_width> flatten;
MSE<input_height * input_width * channels_out> loss_fn;
printf("input x:\n");
print_n(x);
printf("conv weights:\n");
print_n(conv.weights);
printf("conv bias:");
print_n(conv.bias);
auto y1 = conv.forward(x);
auto y = flatten.forward(y1);
auto loss = loss_fn.forward(y_true, y);
printf("output y:\n");
print_n(flatten.backward(y));
printf("loss: %.5f\n", loss);
auto dloss_dy = loss_fn.backward(y_true, y);
auto dloss_dy1 = flatten.backward(dloss_dy);
auto dloss_dx = conv.backward(x, dloss_dy1);
printf("dloss_dy:\n");
print_n(dloss_dy1);
printf("dloss_dx:\n");
print_n(dloss_dx);
conv.train(/*learning_rate */ 1.0);
printf("updated conv weights:\n");
print_n(conv.weights);
printf("updated conv bias:\n");
print_n(conv.bias);
return 0;
}Compiled C++ code output matches Tensorflow output from the Python implementation in this post.
$ g++ -o conv8 -Wall -std=c++2a conv8.cpp && ./conv8
input x:
50.00 49.00 48.00 47.00 46.00
45.00 44.00 43.00 42.00 41.00
40.00 39.00 38.00 37.00 36.00
35.00 34.00 33.00 32.00 31.00
30.00 29.00 28.00 27.00 26.00
25.00 24.00 23.00 22.00 21.00
20.00 19.00 18.00 17.00 16.00
15.00 14.00 13.00 12.00 11.00
10.00 9.00 8.00 7.00 6.00
5.00 4.00 3.00 2.00 1.00
conv weights:
1.00 2.00 3.00
4.00 5.00 6.00
7.00 8.00 9.00
10.00 11.00 12.00
13.00 14.00 15.00
16.00 17.00 18.00
conv bias: 1.00
output y:
2693.00 3761.00 3629.00 3497.00 2165.00
3043.00 4183.00 4012.00 3841.00 2335.00
2443.00 3328.00 3157.00 2986.00 1795.00
1843.00 2473.00 2302.00 2131.00 1255.00
845.00 1097.00 1001.00 905.00 509.00
loss: 7139752.50000
dloss_dy:
215.36 300.80 290.24 279.68 173.12
243.36 334.56 320.88 307.20 186.72
195.36 266.16 252.48 238.80 143.52
147.36 197.76 184.08 170.40 100.32
67.52 87.68 80.00 72.32 40.64
dloss_dx:
3101.28 5677.20 6327.36 5596.08 3838.72
7040.40 12163.68 13369.68 11648.16 7682.32
6822.72 11647.44 12674.88 10928.88 7120.80
5176.56 8722.08 9370.80 7970.40 5119.60
3251.52 5360.40 5660.64 4726.32 2973.28
12948.00 21024.00 22827.60 19616.64 12359.20
21040.80 33936.48 36686.88 31381.92 19643.68
19283.76 30925.44 33125.76 28068.48 17443.44
13833.12 22027.68 23317.92 19513.44 12013.60
7754.40 12240.00 12790.80 10556.16 6426.40
updated conv weights:
-130106.53 -156338.81 -133827.08
-166008.97 -198697.39 -169492.08
-139199.72 -166136.00 -141313.23
-55509.52 -65401.80 -54670.08
-65315.96 -76280.40 -63183.08
-45522.72 -52423.00 -42692.24
updated conv bias:
-4895.32Source code from this example is available at:
References
Online Matrix calculus tool is useful for verifying matrix derivatives