DNN with backpropagation in C++, part 4
Adding sigmoid activation in C++
In this post I’ll modify the previous example adding Sigmoid activation layer.
Previous example can be found at “Dense layer with backpropagation in C++, part 3”
Forward path for the layer is sigmoid function
\[\sigma {(x_{i})} = \frac {1} {1 + e^{-x_{i}}}\]where X is input vector of size M:
\[X = \left( \begin{array}{ccc} x_{0} & x_{1} & \ldots & x_{M-1} \\ \end{array} \right)\]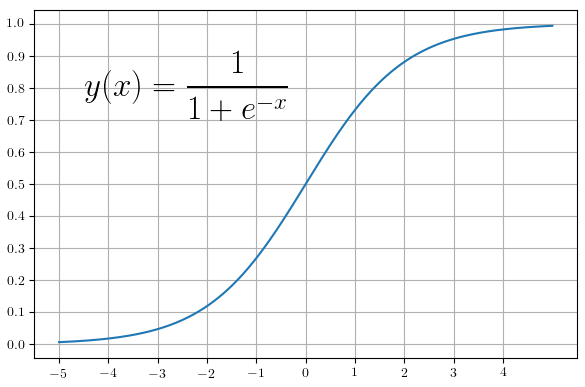
Let’s find sigmoid derivative
\[\frac {\partial {\sigma (x)}} {\partial {x}}\](1) Starting from f(x)
\[f(x) = \frac {1} {\sigma (x)}\] \[\frac {\partial f(x)} {\partial x} = \frac { \partial {\sigma (x)^{-1}}} {\partial x}\] \[\frac {\partial f(x)} {\partial x} = - \frac {1} {\sigma (x)^2} * \frac {\partial {\sigma (x)}} {\partial x}\](2) Also let’s consider
\[f(x) = 1 + e^{-x}\] \[\frac { \partial f(x)} {\partial x} = - e^{-x}\] \[\frac { \partial f(x)} {\partial x} = 1 - f(x)\] \[\frac { \partial f(x)} {\partial x} = 1 - \frac {1} {\sigma{(x)}}\] \[\frac { \partial f(x)} {\partial x} = \frac {\sigma (x) - 1} {\sigma (x)}\]After making (1) and (2) equal, and simplifying
\[- \frac {1} {\sigma (x)^2} * \frac {\partial {\sigma{(x)}}} {\partial{x}} = \frac {\sigma (x) - 1} {\sigma (x)}\]We get final equation for derivative of sigmoid
\[\frac {\partial {\sigma{(x)}}} {\partial x} = \sigma (x) * (1 - \sigma (x))\]Now let’s add sigmoid activation to the source code from the previous Python and C++ examples.
First, let’s modify python code. I’ll use it to validate C++ code in the consecutive section.
Below are package versions I used to buuld and run the examples.
$ python3 -m pip freeze | grep "numpy\|tensorflow"
numpy==1.19.5
tensorflow==2.5.0rc2
$ g++ --version
g++ 9.3.0Import TF and Keras. We’ll define a network with 2 inputs and 2 outpus, 2 Dense layers with bias and sigmoid activaton, and MSE loss function for error backpropagation.
import tensorflow as tf
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam, RMSprop
from tensorflow.keras import backend as K
import numpy as npCreate 2 layer sequential model. Dense layers now have sigmoid activations.
num_inputs = 2
num_outputs = 2
# Create sequential model
model = tf.keras.Sequential()
# No activation
# 1.0 for weights initialization
# 2.0 for bias initialization
layer1 = Dense(units=num_inputs, use_bias=True, activation="sigmoid", weights=[np.ones([num_inputs, num_inputs]), np.full([num_inputs], 2.0)])
layer2 = Dense(units=num_outputs, use_bias=True, activation="sigmoid", weights=[np.ones([num_inputs, num_outputs]), np.full([num_outputs], 2.0)])
model.add(layer1)
model.add(layer2)Use mean square error for the loss function.
# use MSE as loss function
loss_fn = tf.keras.losses.MeanSquaredError()Hardcode model input and expected model output. We’ll use the same array values later in the C++ implementation.
# Arbitrary model input
x = np.array([2.0, 0.5])
# Expected output
y_true = np.array([2.0, 1.0])Use Stochastic Gradient Decent (SGD) optimizer.
SGD weight update rule is
\[W = W - LR * \frac {\partial E} {\partial W}\]\(LR\) is the learning rate.
For now we’ll assume learning rate equal to 1.0
# SGD update rule for parameter w with gradient g when momentum is 0 is as follows:
# w = w - learning_rate * g
#
# For simplicity make learning_rate=1.0
optimizer = tf.keras.optimizers.SGD(learning_rate=1.0, momentum=0.0)In the training loop we’ll compute model output for input X, compute and backpropagate the loss.
# Get model output y for input x, compute loss, and record gradients
with tf.GradientTape(persistent=True) as tape:
# get model output y for input x
# add newaxis for batch size of 1
xt = tf.convert_to_tensor(x[np.newaxis, ...])
tape.watch(xt)
y = model(xt)
# loss gradient with respect to loss input y
dy_dw = tape.gradient(y, model.trainable_variables)
# obtain MSE loss
loss = loss_fn(y_true, y)
# loss gradient with respect to loss input y
dloss_dy = tape.gradient(loss, y)
# adjust Dense layer weights
grad = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grad, model.trainable_variables))Finally we’ll print inputs, outputs, gradients, and updated Dense layer weights.
# print model input and output excluding batch dimention
print(f"input x={x}")
print(f"output y={y[0]}")
print(f"expected output y_true={y_true}")
# print MSE loss
print(f"loss={loss}")
# print loss gradients
print("dloss_dy={}".format(*[v.numpy() for v in dloss_dy]))
# print weight gradients d_loss/d_w
print("grad=\n{}".format(*[v.numpy() for v in grad]))
# print updated dense layer weights
print("updated weights=")
print(*[v.numpy() for v in model.trainable_variables], sep="\n")After running Python example:
$ python3 dense4.py
output y=[0.98162156 0.98162156]
expected output y_true=[2. 1.]
loss=0.5187162160873413
dloss_dy=[-1.0183785 -0.01837844]
grad=
[[-0.00040648 -0.00040648]
[-0.00010162 -0.00010162]]
updated weights=
0) dense/kernel:0
[[1.0004065 1.0004065]
[1.0001016 1.0001016]]
1) dense/bias:0
[2.0002031 2.0002031]
2) dense_1/kernel:0
[[1.0181704 1.000328 ]
[1.0181704 1.000328 ]]
3) dense_1/bias:0
[2.0183723 2.0003316]Output of Python dense4.py will be used to validate C++ implementation. Let’s code the same example in C++. We’ll introduce new Sigmoid layer with forward and backward path.
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cassert>
#include <numeric>
#include <array>
#include <chrono>
#include <iostream>
#include <string>
#include <functional>
#include <array>
#include <iterator>
using namespace std;
using std::chrono::high_resolution_clock;
using std::chrono::duration_cast;
using std::chrono::microseconds;Lambda will be used to pretty print inputs, outputs, and layer weights.
/*
* Print helper function
*/
constexpr auto print_fn = [](const float& x) -> void {printf("%.7f ", x);};Dense layer weights initializer.
/*
* Constant weight intializer
*/
const float const_one = 1.0;
const float const_two = 2.0;
template<float const& value = const_one>
constexpr auto const_initializer = []() -> float
{
return value;
};Dense layer class template includes forward() and backward() functions. forward() was modified from the previous example to add bias in output computation. Backward() function was modified from the previous example to update bias with input gradient.
/*
* Dense layer class template
*
* Parameters:
* num_inputs: number of inputs to Dense layer
* num_outputs: number of Dense layer outputs
* T: input, output, and weights type in the dense layer
* initializer: weights initializer function
*/
template<size_t num_inputs, size_t num_outputs, typename T = float,
T (*weights_initializer)() = const_initializer<const_one>,
T (*bias_initializer)() = const_initializer<const_two> >
struct Dense
{
typedef array<T, num_inputs> input_vector;
typedef array<T, num_outputs> output_vector;
vector<input_vector> weights;
output_vector bias;
/*
* Dense layer constructor
*/
Dense()
{
/*
* Create num_outputs x num_inputs weights matrix
*/
weights.resize(num_outputs);
for (input_vector& w: weights)
{
generate(w.begin(), w.end(), *weights_initializer);
}
/*
* Initialize bias vector
*/
generate(bias.begin(), bias.end(), *bias_initializer);
}
/*
* Dense layer forward pass
*/
output_vector forward(const input_vector& x)
{
/*
* Check for input size mismatch
*/
assert(x.size() == weights[0].size());
/*
* Layer output is dot product of input with weights
*/
output_vector activation;
transform(weights.begin(), weights.end(), bias.begin(), activation.begin(),
[x](const input_vector& w, T bias)
{
T val = inner_product(x.begin(), x.end(), w.begin(), 0.0) + bias;
return val;
}
);
return activation;
}
/*
* Dense layer backward pass
*/
input_vector backward(input_vector& input, output_vector grad)
{
/*
* Weight update according to SGD algorithm with momentum = 0.0 is:
* w = w - learning_rate * d_loss/dw
*
* For simplicity assume learning_rate = 1.0
*
* d_loss/dw = dloss/dy * dy/dw
* d_loss/dbias = dloss/dy * dy/dbias
*
* dloss/dy is input gradient grad
*
* dy/dw is :
* y = w[0]*x[0] + w[1] * x[1] +... + w[n] * x[n] + bias
* dy/dw[i] = x[i]
*
* dy/dbias is :
* dy/dbias = 1
*
* For clarity we:
* assume learning_rate = 1.0
* first compute dw
* second update weights by subtracting dw
*/
/*
* compute dw
* dw = outer(x, grad)
*/
vector<input_vector> dw;
for (auto grad_i: grad)
{
auto row = input;
for_each(row.begin(), row.end(), [grad_i](T &xi){ xi *= grad_i;});
dw.push_back(row);
}
/*
* Compute backpropagated gradient
*/
input_vector ret;
transform(weights.begin(), weights.end(), ret.begin(),
[grad](input_vector& w)
{
T val = inner_product(w.begin(), w.end(), grad.begin(), 0.0);
return val;
});
/*
* compute w = w - dw
* assume learning rate = 1.0
*/
transform(weights.begin(), weights.end(), dw.begin(), weights.begin(),
[](input_vector& left, input_vector& right)
{
transform(left.begin(), left.end(), right.begin(),
left.begin(),
minus<T>());
return left;
});
/*
* compute bias = bias - grad
* assume learning rate = 1.0
*/
transform(bias.begin(), bias.end(), grad.begin(), bias.begin(),
[](const T& bias_i, const T& grad_i)
{
return bias_i - grad_i;
});
return ret;
}
/*
* Helper function to convert Dense layer to string
* Used for printing the layer weights and biases
*/
operator std::string() const
{
std::ostringstream ret;
ret.precision(7);
/*
* output weights
*/
ret << "weights:" << std::endl;
for (int y=0; y < weights[0].size(); y++)
{
for (int x=0; x < weights.size(); x++)
{
if (weights[x][y] >= 0)
ret << " ";
ret << std::fixed << weights[x][y] << " ";
}
ret << std::endl;
}
/*
* output biases
*/
ret << "bias:" << std::endl;
for (auto b: bias)
{
if (b >= 0)
ret << " ";
ret << std::fixed << b << " ";
}
ret << std::endl;
return ret.str();
}
/*
* Helper function to cout Dense layer object
*/
friend ostream& operator<<(ostream& os, const Dense& dense)
{
os << (string)dense;
return os;
}
};Sigmoid layer class template includes forward() and backward() functions. forward() computes sigmoid(x) = 1 / (1 + exp(-x)) backward() computes mutiple of gradient and sigmoid derivative wrt input.
/*
* Sigmoid layer class template
*/
template<size_t num_inputs, typename T = float>
struct Sigmoid
{
typedef array<T, num_inputs> input_vector;
static input_vector forward(const input_vector& y)
{
input_vector ret;
transform(y.begin(), y.end(), ret.begin(),
[](const T& yi)
{
T out = 1.0 / (1.0 + expf(-yi));
return out;
});
return ret;
}
static input_vector backward(const input_vector& y, const input_vector grad)
{
input_vector ret;
transform(y.begin(), y.end(), grad.begin(), ret.begin(),
[](const T& y_i, const T& grad_i)
{
T s = 1.0 / (1.0 + expf(-y_i));
T out = grad_i * s * (1 - s);
return out;
});
return ret;
}
};Mean Squared Error class will need it’s own forward and backward functions.
/*
* Mean Squared Error loss class
* Parameters:
* num_inputs: number of inputs to MSE function.
* T: input type, float by defaut.
*/
template<size_t num_inputs, typename T = float>
struct MSE
{
/*
* Forward pass computes MSE loss for inputs y (label) and yhat (predicted)
*/
static T forward(const array<T, num_inputs>& y, const array<T, num_inputs>& yhat)
{
T loss = transform_reduce(y.begin(), y.end(), yhat.begin(), 0.0, plus<T>(),
[](const T& left, const T& right)
{
return (left - right) * (left - right);
}
);
return loss / num_inputs;
}
/*
* Backward pass computes dloss/dy for inputs y (label) and yhat (predicted)
*
* loss = sum((yhat[i] - y[i])^2) / N
* i=0...N-1
* where N is number of inputs
*
* d_loss/dy[i] = 2 * (yhat[i] - y[i]) * (-1) / N
* d_loss/dy[i] = 2 * (y[i] - yhat[i]) / N
*
*/
static array<T, num_inputs> backward(const array<T, num_inputs>& y,
const array<T, num_inputs>& yhat)
{
array<T, num_inputs> de_dy;
transform(y.begin(), y.end(), yhat.begin(), de_dy.begin(),
[](const T& left, const T& right)
{
return 2 * (right - left) / num_inputs;
}
);
return de_dy;
}
};Finally, in the main function, we’ll declare input x and expecetd output y_true arrays, containing the same values as in out Python example. Then we’ll compute forward and backward passes, and print the network output and updated weights.
int main(void)
{
const int num_inputs = 2;
const int num_outputs = 2;
const int num_iterations = 1000;
array<float, num_inputs> x = {2.0, 0.5};
array<float, num_outputs> ytrue = {2.0, 1.0};
/*
* Create dense layer and MSE loss
*/
Dense<num_inputs, num_outputs> dense1;
Dense<num_inputs, num_outputs> dense2;
Sigmoid<num_outputs> sigmoid1;
Sigmoid<num_outputs> sigmoid2;
MSE<num_outputs> mse_loss;
/*
* Compute Dense layer output y for input x
*/
auto y1 = dense1.forward(x);
auto y2 = sigmoid1.forward(y1);
auto y3 = dense2.forward(y2);
auto y4 = sigmoid2.forward(y3);
/*
* Compute MSE loss for output y4 and label ytrue
*/
auto loss = mse_loss.forward(ytrue, y4);
/*
* Benchmark Dense layer inference latency
*/
auto ts = high_resolution_clock::now();
for (auto iter = 0; iter < num_iterations; iter++)
{
y1 = dense1.forward(x);
}
auto te = high_resolution_clock::now();
auto dt_us = (float)duration_cast<microseconds>(te - ts).count() / num_iterations;
/*
* Print DNN input x
*/
printf("input x=");
for_each(x.begin(), x.end(), print_fn);
printf("\n");
/*
* Print DNN output y
*/
printf("output y=");
for_each(y4.begin(), y4.end(), print_fn);
printf("\n");
/*
* Print loss
*/
printf("loss: %f\n", loss);
/*
* Compute dloss/dy gradients
*/
auto dloss_dy = mse_loss.backward(ytrue, y4);
/*
* Back propagate loss
*/
auto bw4 = sigmoid2.backward(y3, dloss_dy);
auto bw3 = dense2.backward(y2, bw4);
auto bw2 = sigmoid1.backward(y1, bw3);
dense1.backward(x, bw2);
/*
* print dloss/dy
*/
printf("d(loss)/dy: ");
for_each(dloss_dy.begin(), dloss_dy.end(), print_fn);
printf("\n");
/*
* Print updated Dense layer weights
*/
printf("updated dense 1 layer weights:\n%s", ((string)dense1).c_str());
printf("updated dense 2 layer weights:\n%s", ((string)dense2).c_str());
/*
* Print average latency
*/
printf("time dt=%f usec\n", dt_us);
return 0;
}After compiling and running C++ example:
$ g++ -o dense4 -std=c++2a dense4.cpp && ./dense4
input x=2.0000000 0.5000000
output y=0.9816215 0.9816215
loss: 0.518716
d(loss)/dy: -1.0183785 -0.0183785
updated dense 1 layer weights:
weights:
1.0004065 1.0004065
1.0001016 1.0001016
bias:
2.0002031 2.0002031
updated dense 2 layer weights:
weights:
1.0181705 1.0003279
1.0181705 1.0003279
bias:
2.0183723 2.0003316
time dt=0.102000 usecAs one can verify, forward path output of the C++ implementation matches the Python code. Also, weights and biases of dense layers after backpropagation match in Python and C++ code.
Python source code for this example is at dense4.py
C++ implementation is at dense4.cpp