DNN with backpropagation in C++, part 1
Dense layer with backpropagation in C++
Let’s code a DNN in C++. Initially we’ll try to keep it as simple as possible. The network will consist of a single fully connected Dense layer. It should support forward and back propagation. We assume:
- there’s no bias in the dense layer;
- there’s no non-linear activation;
- loss function is Mean Squared Error.
Forward path for input vector X of size M, and dense layer with \(M\) inputs and \(N\) outputs
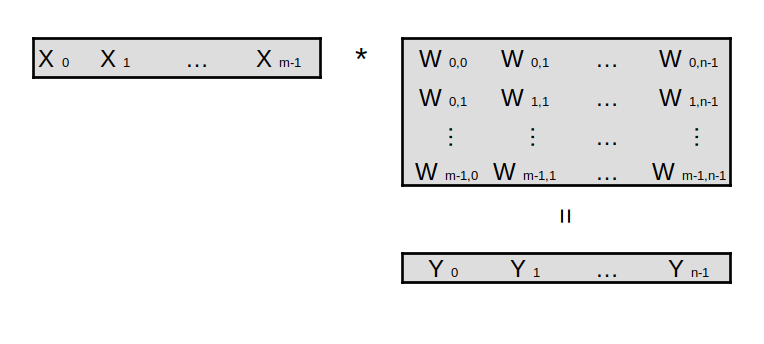
Dense layer output Y is matrix multiplication of X by W:
\[\hat Y = X W\]Where:
\(\hat Y\) is predicted output vector:
\[\hat Y = \left( \begin{array}{ccc} \hat y_{0} & \hat y_{1} & \ldots & \hat y_{N-1} \\ \end{array} \right)\]\(X\) is input vector:
\[X = \left( \begin{array}{ccc} x_{0} & x_{1} & \ldots & x_{M-1} \\ \end{array} \right)\]\(W\) is weights matrix:
\[W = \left( \begin{array}{ccc} w_{0,0} & w_{0,1} & \ldots & w_{0,N-1} \\ w_{1,0} & w_{1,1} & \ldots & w_{1,N-1} \\ \vdots & \vdots & \ldots & \vdots \\ w_{M-1,0} & w_{M-1,1} & \ldots & w_{M-1,N-1} \\ \end{array} \right)\]Mean Squared Error (MSE) loss between predicted output \(\hat Y\) and expected output \(Y\) :
\[E (Y, \hat Y) = \frac {1} {N} \sum_{i=0}^{N-1} ( Y_{i} - \hat Y_{i} )^2\]Where \(Y\) is expected output vector:
\[Y = \left( \begin{array}{ccc} y_{0} & y_{1} & \ldots & y_{N-1} \\ \end{array} \right)\]Error backpropagation
For input \(X\), we want to minimize the MSE difference between out network output and expected output, by adjusting dense layer weights by error gradient \(\frac {\partial E} {\partial W}\)
\[W_{t+1} = W_{t} - \alpha * \frac {\partial E} {\partial W}\]Here \(\alpha\) is learning rate
and \(\frac {\partial E} {\partial W}\) is error gradient with regards to weights.
Lets find error gradient \(\frac {\partial E} {\partial W}\)
Using chain rule
\[\hat Y = X * W\] \[\frac {\partial E (\hat Y) } {\partial W} = \frac {\partial E} {\partial \hat Y} * \frac {\partial \hat Y} {\partial W}\]where
\[\frac {\partial E} {\partial \hat Y} = \frac {2} {N} ( \hat {Y} - Y )\]and
\[\frac {\partial \hat Y} {\partial W} = \frac {\partial (X W)} {\partial W} = X^T\]Finally, weights update \(\frac {\partial E} {\partial W}\) is:
\[\frac {\partial E} {\partial W} = \frac {2} {N} ( \hat {Y} - Y ) * X^T\] \[\frac {\partial E} {\partial W} = \frac {2} {N} ( \hat {Y} - Y ) \otimes X\]Let’s write Python implementation with TF2/Keras. We’ll use it to validate C++ code in the consecutive section.
For this experiment I’ve used the following software versions:
$ python3 -m pip freeze | grep "numpy\|tensorflow"
numpy==1.19.5
tensorflow==2.5.0rc2
$ g++ --version
g++ 9.3.0Import TF and Keras. We’ll define a network with 3 inputs and 2 outpus.
import tensorflow as tf
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import RMSprop
import numpy as np
num_inputs = 3
num_outputs = 2Define Keras sequential network with single Dense layer.
# Create one layer model
model = tf.keras.Sequential()
# No bias, no activation, initialize weights with 1.0
model.add(Dense(units=num_outputs, use_bias=False, activation=None, kernel_initializer=tf.keras.initializers.ones()))Use mean square error for the loss function.
# use MSE as loss function
loss_fn = tf.keras.losses.MeanSquaredError()Hardcode model iput and expected model output. We’ll use the same array values later in C++ implementation.
# Arbitrary model input
x = np.array([2.0, 0.5, 1])
# Expected output
y_true = np.array([1.5, 1.0])Use Stochastic Gradient Decent (SGD) optimizer.
SGD weight update rule is \(W = W - LR * \nabla\)
\(\nabla\) is weight gradient and \(LR\) is learning rate.
For now we’ll assume learning rate equal to 1.0
# SGD update rule for parameter w with gradient g when momentum is 0 is as follows:
# w = w - learning_rate * g
#
# For simplicity make learning_rate=1.0
optimizer = tf.keras.optimizers.SGD(learning_rate=1.0, momentum=0.0)In the training loop we’ll compute model output for input X, compute and backpropagate the loss.
# Get model output y for input x, compute loss, and record gradients
with tf.GradientTape(persistent=True) as tape:
# get model output y for input x
# add newaxis for batch size of 1
xt = tf.convert_to_tensor(x[np.newaxis, ...])
tape.watch(xt)
y = model(xt)
# obtain MSE loss
loss = loss_fn(y_true, y)
# loss gradient with respect to loss input y
dloss_dy = tape.gradient(loss, y)
# adjust Dense layer weights
grad = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grad, model.trainable_variables))Finally we’ll print inputs, outputs, gradients, and updated Dense layer weights.
# print model input and output excluding batch dimention
print(f"input x={x}")
print(f"output y={y[0]}")
print(f"expected output y_true={y_true}")
# print MSE loss
print(f"loss={loss}")
# print loss gradients
print(f"dloss_dy={dloss_dy[0].numpy()}")
# print weight gradients d_loss/d_w
print(f"grad=\n{grad[0].numpy()}")
# print updated dense layer weights
print(f"vars=\n{model.trainable_variables[0].numpy()}")After running Python example we get:
$ python3 dense.py
input x=[2. 0.5 1. ]
output y=[3.5 3.5]
expected output y_true=[1.5 1. ]
loss=5.125
dloss_dy=[2. 2.5]
grad=
[[4. 5. ]
[1. 1.25]
[2. 2.5 ]]
vars=
[[-3. -4. ]
[ 0. -0.25]
[-1. -1.5 ]]Let’s code the same example in C++
We’ll implement it using C++ STL. Chrono headers are included for clocks used to benchmark run time.
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cassert>
#include <numeric>
#include <array>
#include <chrono>
#include <iostream>
#include <string>
#include <functional>
#include <array>
#include <iterator>
using namespace std;
using std::chrono::high_resolution_clock;
using std::chrono::duration_cast;
using std::chrono::microseconds;Dense layer weights initializer
/*
* Constant 1.0 weight intializer
*/
static auto ones_initializer = []() -> float
{
return 1.0;
};Dense layer class template includes forward() and backward() functions.
/*
* Dense layer class template
*
* Parameters:
* num_inputs: number of inputs to Dense layer
* num_outputs: number of Dense layer outputs
* T: input, output, and weights type in the dense layer
* initializer: weights initializer function
*/
template<size_t num_inputs, size_t num_outputs, typename T = float,
T (*initializer)()=ones_initializer>
struct Dense
{
typedef array<T, num_inputs> input_vector;
typedef array<T, num_outputs> output_vector;
/*
* Layer weights
*/
vector<input_vector> weights;
/*
* Dense class constructor
*/
Dense()
{
/*
* Create num_outputs x num_inputs matric
*/
weights.resize(num_outputs);
for (input_vector& w: weights)
{
generate(w.begin(), w.end(), *initializer);
}
}
/*
* Dense forward pass
*/
array<T, num_outputs> forward(const input_vector& x)
{
/*
* Check for input size mismatch
*/
assert(x.size() == weights[0].size());
/*
* Layer output is dot product of input with weights
*/
array<T, num_outputs> activation;
transform(weights.begin(), weights.end(), activation.begin(),
[x](const input_vector& w)
{
T val = inner_product(x.begin(), x.end(), w.begin(), 0.0);
return val;
}
);
return activation;
}
/*
* Dense layer backward pass
*/
void backward(const input_vector& input, const output_vector& dloss_dy)
{
/*
* Weight update according to SGD algorithm with momentum = 0.0 is:
* w = w - learning_rate * d_loss/dw
*
* For simplicity assume learning_rate = 1.0
*
* d_loss/dw = dloss/dy * dy/dw
*
* dy/dw is :
* y = w[0]*x[0] + w[1] * x[1] +... + w[n] * x[n]
* dy/dw[i] = x[i]
*
* For clarity we:
* assume learning_rate = 1.0
* first compute dw
* second update weights by subtracting dw
*/
/*
* compute dw
* dw = outer(x, de_dy)
*/
vector<input_vector> dw;
for (auto const& dloss_dyi: dloss_dy)
{
auto row = input;
for_each(row.begin(), row.end(), [dloss_dyi](T &xi){ xi *= dloss_dyi;});
dw.emplace_back(row);
}
/*
* compute w = w - dw
* assume learning rate = 1.0
*/
transform(weights.begin(), weights.end(), dw.begin(), weights.begin(),
[](input_vector& left, const input_vector& right)
{
transform(left.begin(), left.end(),
right.begin(),
left.begin(),
minus<T>());
return left;
}
);
}
/*
* Helper function to convert Dense layer to string
* Used for printing the layer weights
*/
operator std::string() const
{
string ret;
for (int y=0; y < weights[0].size(); y++)
{
for (int x=0; x < weights.size(); x++)
{
ret += to_string(weights[x][y]) + " ";
}
ret += "\n";
}
return ret;
}
/*
* Helper function to cout Dense layer weights
*/
friend ostream& operator<<(ostream& os, const Dense& dense)
{
os << (string)dense;
return os;
}
};Mean Squared Error class will need it’s own forward and backward functions.
/*
* Mean Squared Error loss class
* Parameters:
* num_inputs: number of inputs to MSE function.
* T: input type, float by defaut.
*/
template<size_t num_inputs, typename T = float>
struct MSE
{
/*
* Forward pass computes MSE loss for inputs y (label) and yhat (predicted)
*/
static T forward(const array<T, num_inputs>& y, const array<T, num_inputs>& yhat)
{
T loss = transform_reduce(y.begin(), y.end(), yhat.begin(), 0.0, plus<T>(),
[](const T& left, const T& right)
{
return (left - right) * (left - right);
}
);
return loss / num_inputs;
}
/*
* Backward pass computes dloss/dy for inputs y (label) and yhat (predicted)
*
* loss = sum((yhat[i] - y[i])^2) / N
* i=0...N-1
* where N is number of inputs
*
* d_loss/dy[i] = 2 * (yhat[i] - y[i]) * (-1) / N
* d_loss/dy[i] = 2 * (y[i] - yhat[i]) / N
*
*/
static array<T, num_inputs> backward(const array<T, num_inputs>& y,
const array<T, num_inputs>& yhat)
{
array<T, num_inputs> de_dy;
transform(y.begin(), y.end(), yhat.begin(), de_dy.begin(),
[](const T& left, const T& right)
{
return 2 * (right - left) / num_inputs;
}
);
return de_dy;
}
};Finally, in the main function, we’ll declare input x and expecetd output y_true arrays, containing the same values as in out Python example. Then we’ll compute forward and backward passes, and print the network output and updated weights.
int main(void)
{
const int num_inputs = 3;
const int num_outputs = 2;
const int num_iterations = 1000;
auto print_fn = [](const float& x) -> void {printf("%.5f ", x);};
array<float, num_inputs> x = {2.0, 0.5, 1.0};
array<float, num_outputs> y_true = {1.5, 1.0};
/*
* Create dense layer and MSE loss
*/
Dense<num_inputs, num_outputs> dense;
MSE<num_outputs> mse_loss;
/*
* Compute Dense layer output y for input x
*/
auto yhat = dense.forward(x);
/*
* Copute MSE loss for output y and expected y_true
*/
auto loss = mse_loss.forward(y_true, yhat);
/*
* Run inference 1000 times and benchmark dense layer latency
*/
auto ts = high_resolution_clock::now();
for (auto iter = 0; iter < num_iterations; iter++) [[likely]] dense.forward(x);
auto te = high_resolution_clock::now();
auto dt_us = (float)duration_cast<microseconds>(te - ts).count() / num_iterations;
/*
* Print DNN input x
*/
printf("input x=");
for_each(x.begin(), x.end(), print_fn);
printf("\n");
/*
* Print DNN output y
*/
printf("outut y=");
for_each(yhat.begin(), yhat.end(), print_fn);
printf("\n");
/*
* Print expected output y_true
*/
printf("expected outut y=");
for_each(y_true.begin(), y_true.end(), print_fn);
printf("\n");
/*
* Print loss for output y and label y_true
*/
printf("loss: %f\n", loss);
/*
* Compute dloss/dy gradients
*/
auto dloss_dy = mse_loss.backward(y_true, yhat);
/*
* Back propagate loss
*/
dense.backward(x, dloss_dy);
/*
* print dloss/dy
*/
printf("loss gradient: ");
for_each(dloss_dy.begin(), dloss_dy.end(), print_fn);
printf("\n");
/*
* Print updated Dense layer weights
*/
printf("updated dense layer weights:\n%s", ((string)dense).c_str());
/*
* Print average latency
*/
printf("time dt=%f usec\n", dt_us);
return 0;
}After compiling and running C++ example we get:
input x=2.00000 0.50000 1.00000
outut y=3.50000 3.50000
expected outut y=1.50000 1.00000
loss: 5.125000
loss gradient: 2.00000 2.50000
updated dense layer weights:
-3.000000 -4.000000
0.000000 -0.250000
-1.000000 -1.500000
time dt=0.093000 usecAs one can verify, forward path output of the C++ implementation matches the Python code. Also, gradients and Dense layer weights after backpropagation match in Python and C++ code.
Python source code for this example is at dense.py
C++ implementation is at dense.cpp